5. FUNKCIJE ENE SPREMENJLIVKE
5.1 Osnovne lastnosti
Preslikava (funkcija, upodobitev, transformacija) iz množice v množico je tako pravilo, ki vsakemu elementu iz prve množice priredi element iz druge množice, .
Množici pravimo definicijsko območje (domena) preslikave, njenim elementom pa originali. V množici seveda niso vedno vsi elementi slike elementov množice . Tisti elementi, ki to so, tvorijo podmnožico množice . To podmnožico imenujemo zaloga vrednosti preslikave.
V analizi običajno obravnavamo realne funkcije, pri katerih je domena in kodomena množica realnih števil. Tako nas bodo v nadaljevanju zanimale preslikave , za katere bomo običajno uporabljali izraz funkcija. Torej, funkcija , definirana na intervalu ( ), je predpis, po katerem pripada vsakemu številu s tega intervala natanko določeno število . število običajno označimo s simbolom ( ) in ga imenujemo vrednost funkcije za določeni . Pravimo, da je neodvisna spremenljivka ali argument funkcije, število pa odvisna spremenljivka.
Oznaki: definicijsko območje funkcije , zaloga vrednosti funkcije ,
.
Primer 5.1:
1. Naj bo . Definicijsko območje in zaloga vrednosti so vsa realna števila,
|
2. če vsakemu realnemu številu iz intervala priredimo število , dobimo funkcijo s predpisom
Slika 5.1: |
3. Naj bo funkcija definirana s predpisom ( , ). To funkcijo imenujemo kvadratna funkcija, njeno definicijsko območje je množica vseh realnih števil, zaloga vrednosti pa vsa pozitivna realna števila,
|
4. Naj bo . Potem je
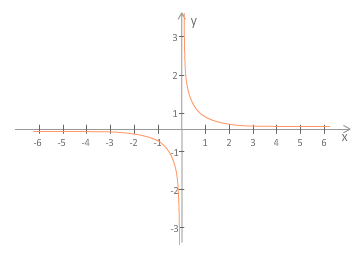
Slika 5.2: |
5. Naj bo . Torej je , iz česar sledi . Potem je
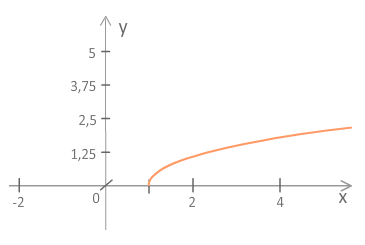
Slika 5.3: |
***
Definicija 5.2: Funkcija definirana na simetričnem intervalu ( ali ) je soda, ko je
in je liha, ko je
***
Primer 5.3:
1. Naj bo . Ker je , je soda funkcija. 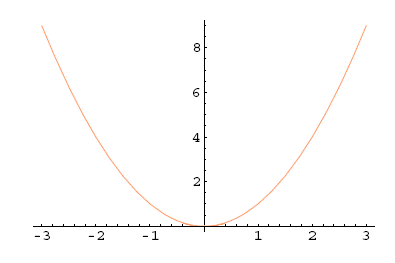
Slika 5.4: |
2. Naj bo . Ker je , je liha funkcija. 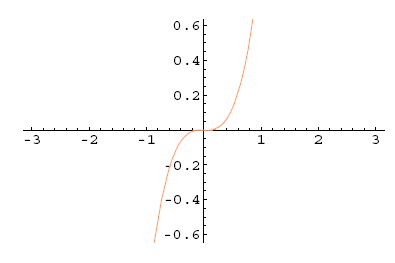
Slika 5.5: |
3. Funkcija definirana s predpisom ni niti soda niti liha, saj je in . 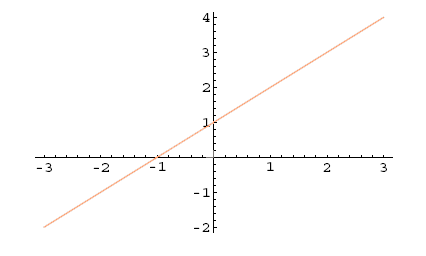
Slika 5.6: |
4. Funkcija je soda, pa liha funkcija. |
Graf sode funkcije je simetričen glede na os, graf lihe funkcije pa je simetričen glede na koordinatno izhodišče.
***
Definicija 5.4: Naj bo definirana na intervalu in naj bosta . Funkcija je naraščajoča, ko je
in je strogo naraščajoča, ko je
Funkcija je padajoča, ko je
in je strogo padajoča, ko je
če je funkcija (strogo) naraščajoča ali (strogo) padajoča funkcija, je monotona funkcija.
***
Primer 5.5:
1. Naj bo . Funkcija je monotona funkcija, saj je naraščajoča. 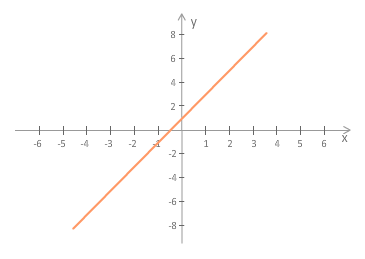
Slika 5.7: |
2. Naj bo . Na intervalu je funkcija padajoča, na intervalu pa naraščajoča. 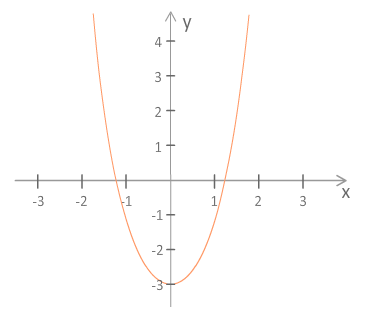
Slika 5.8: |
3. Funkcija , podana s predpisom , je monotona, saj je naraščajoča. 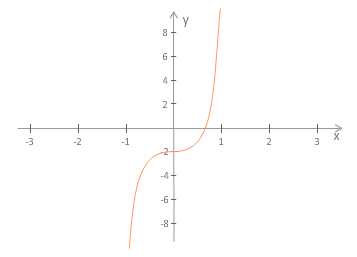
Slika 5.9: |
***
Definicija 5.6: Če obstaja tako število , da je
potem je periodična funkcija s periodo . Najmanjšo pozitivno periodo imenujemo osnovna perioda.
***
Primer 5.7:
1. Naj bo . Ker je , je periodična funkcija z osnovno periodo . |
2. Naj bo . Ker je , je periodična funkcija z osnovno periodo . |
***
5.2 Pregled elementarnih funkcij
5.2.1 Polinomi
Polinomi so funkcije s predpisom oblike
kjer je (konstanta) za vsak če je , pravimo, da je polinom stopnje . številu pravimo vodilni koeficient polinoma, številu pa splošni člen.
Rešitvam polinomske enačbe
pravimo koreni polinoma . Običajno namesto o korenih govorimo kar o ničlah polinoma. Osnovni izrek algebre trdi, da ima polinomska enačba vsaj eno rešitev (v obsegu kompleksnih števil). Glede na ta izrek se izpelje, da ima polinom stopnje natanko ničel, ki pripadajo množici ali . Ker kompleksne ničle zgornje enačbe zmeraj nastopajo v konjugiranih parih, ima polinom lihe stopnje vsaj eno realno ničlo.
Naj bodo (ne nujno različne) ničle polinoma Potem lahko zapišemo kot produkt faktorjev
Če se faktor pojavi -krat v razcepu, pravimo, da je -kratna ničla polinoma (npr. ).
Primer 5.8: Polinom je četrte stopnje in ga lahko zapišemo kot
.
Polinom ima štiri ničle: , , , .
***
Korene polinoma druge stopnje
( ) iščemo po formulah
Izraz pod korenom imenujemo diskriminanta in jo označujemo z
Glede na vrednost diskriminante ločimo tri možnosti:
Primer 5.9
Naj bo . Potem je Ničli sta in
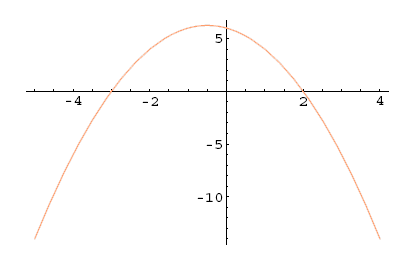
Slika 5.10: ,
***
Primer 5.10
Naj bo . Potem je . Ničla je .
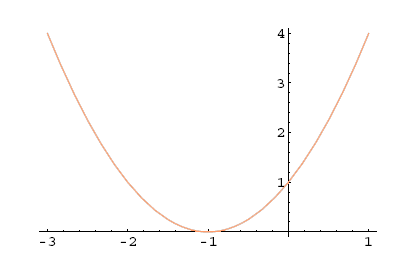
Slika 5.11: ,
***
Primer 5.11
Naj bo . Ker je , polinom nima realnih ničel.
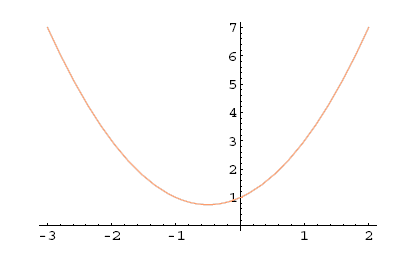
Slika 5.12: ,
***
Korene polinomov višje stopnje
iščemo s pomočjo Hornerjevega algoritma. Uporabimo ga lahko, če poznamo vsaj eno ničlo enačbe . če so koeficienti celoštevilski in je ničla polinoma racionalno število , tedaj deli , pa .
Primer 5.12: Poiščimo vse ničle polinoma
če je koren racionalno število , tedaj je in . Skupaj imamo kandidatov za koren, poleg tega pa še njihove nasprotne vrednosti. S Hornerjevim algoritmom preverimo, da je koren polinoma:
|
|
|
|
|
|
|
|
|
|
|
|
Torej je
Ničle so , , .
***
Kvocient dveh polinomov in je racionalna funkcija
Racionalna funkcija je definirana povsod, kjer je . Ničle ima tam, kjer je .
Primer 5.13: Funkcija
ima enake ničle kot polinom v prejšnjem primeru, definicijsko območje pa je .
***
Primer 5.14
Naj bo .
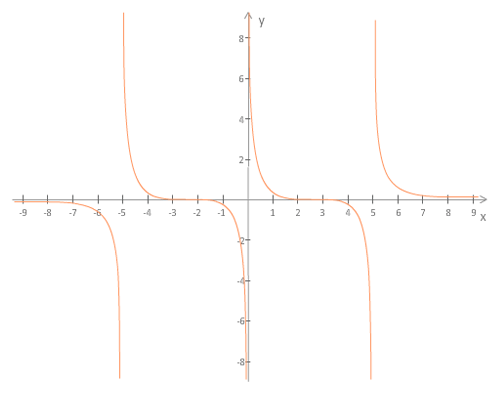
Slika 5.13:
***
5.2.2 Trigonometrijske funkcije
Definirali bomo trigonometrijske funkcije sinus, kosinus, tangens in kotangens, in sicer najprej za kote na intervalu .
Na enotski krožnici (s polmerom in središčem v koordinatnem izhodi šču) si izberemo poljubno točko . če skozi to točko potegnemo poltrak z začetkom v koordinatnem izhodišču, je med tem poltrakom in med pozitivno smerjo osi določen natanko en kot, ki ga ozna čimo z (dogovorimo se, da bomo kote vedno merili od pozitivnega dela osi v smeri nasprotni gibanju urinega kazalca).
Kotne funkcije definiramo:
Sledi, da je
Za poljubne kote definiramo trigonometrijske funkcije na sledeč način:
kjer je poljubno celo število ( ). Opazimo, da so vse štiri funkcije periodične, prvi dve z osnovno periodo , drugi dve pa z osnovno periodo .
Nadalje, kosinus je soda funkcija, , sinus pa je liha funkcija, . Sledi, da sta tangens in kotangens lihi funkciji, , .
Poglejmo si še nekaj najpogostejših zvez med kotnimi funkcijami. Po Pitagorovem izreku velja, da je
Izračunajmo
Podobno velja za kotangens, zato imamo zvezi
Zapišimo še adicijska izreka
Od tod izpeljemo
Iz adicijskih izrekov izpeljemo tudi sinus in kosinus dvojnih kotov
Prav tako nam adicijski izreki dajo naslednji zvezi:
Podobno velja
Poglejmo si grafe trigonometrijskih funkcij. Kosinus in sinus sta definirana na celem , medtem ko tangens ni definiran v ničlah cosinusa ( ), kotangens pa v ničlah sinusa ( ).
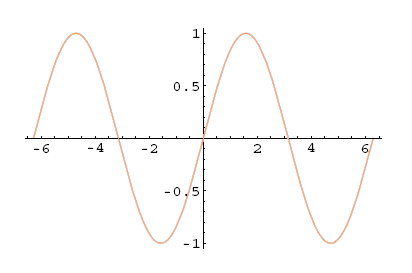
Slika 5.14:
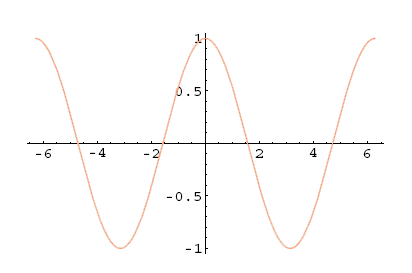
Slika 5.15:
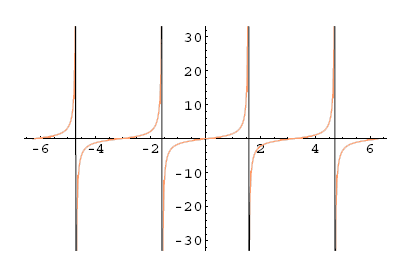
Slika 5.16:
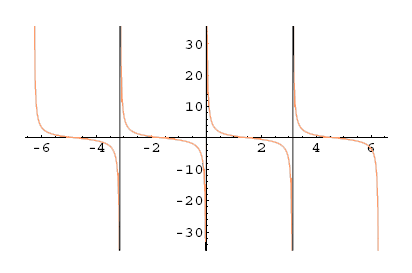
Slika 5.17:
5.2.3 Krožne funkcije
Krožne funkcije so obratne funkcije od trigonometrijskih. Imenujemo jih arkus sinus (arcsin x), arkus kosinus (arccos x), arkus tangens (arctan x), arkus kotangens (arccot x).
1. Arkus sinus
Če želimo, da bo obstajal obrat funkcije sinus, mora le ta biti bijektivna. V ta namen moramo skrčiti definicijsko območje. Naj bo in . Tedaj obstaja taka funkcija , da je
Funkcijo imenujemo arkus sinus in pišemo
Torej velja
Funkcijo imenujemo tudi glavna veja funkcije , stranske pa so na drugih intervalih. Graf obratne funkcije dobimo z zrcaljenjem preko premice .
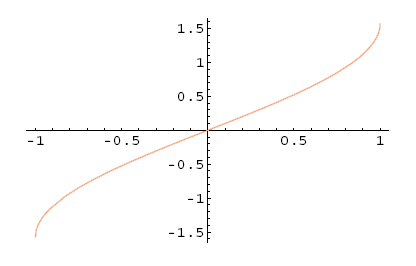
Slika 5.18:
2. Arkus kosinus
Naj bo . Definicijsko območje skrčimo na . Tedaj obstaja in pišemo
Velja
Graf glavne veje funkcije je:
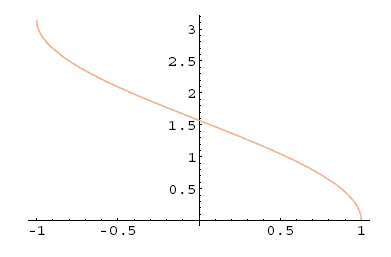
Slika 5.19:
Izpeljimo še zvezo med obema znanima obratnima funkcijama. Naj bo . Tedaj je in . Vemo, da je
kar pomeni, da je
oziroma
3. Arkus tangens
Naj bo . Definicijsko območje skrčimo na . Tedaj obstaja in pišemo
Potemtakem velja
Graf glavne veje funkcije je:
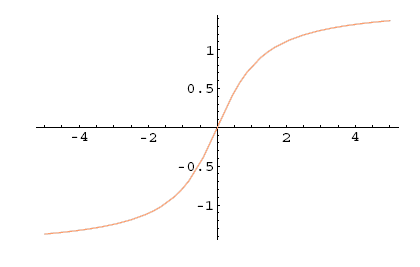
Slika 5.20:
4. Arkus kotangens
Naj bo . Definicijsko območje skrčimo na . Tedaj obstaja . Pišemo
in velja
Izpeljimo še zvezo med obema obratnima funkcijama. Naj bo in . Tedaj je
Torej je
in zato
5.2.4 Eksponentna funkcija
Eksponentna funkcija je oblike
Funkcija je tako imenovana, ker nastopa neodvisna spremenljivka v eksponentu. Ker je , naj bo osnova . Eksponentna funkcija je definirana povsod in je povsod pozitivna ( ).
Velja
saj je
1. Za je strogo naraščajoča funkcija, saj velja:
Primer 5.15: Graf eksponentne funkcije
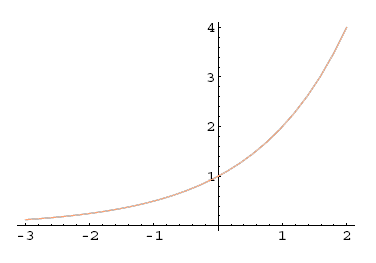
Slika 5.21:
***
2. Za je strogo padajoča funkcija, saj velja:
Primer 5.16: Graf eksponentne funkcije
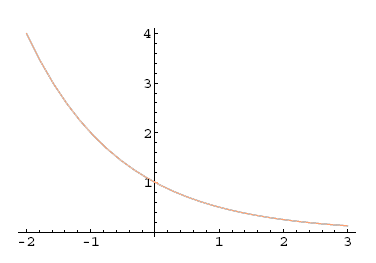
Slika 5.22:
***
5.2.5 Logaritemska funkcija
Naj bo eksponentna funkcija, torej
To je bijektivna funkcija, zato obstaja njej obratna funkcija . Imenujemo jo logaritemska funkcija in pišemo
Torej velja
in
Potemtakem velja:
Logaritemska funkcija ima ničlo v točki 1, saj velja
Izpeljimo nekaj lastnosti logaritma:
1. , ,
2. , ,
3. , , ,
Kadar je osnova enaka številu , govorimo o naravnem logaritmu in pišemo
Graf logaritemske funkcije dobimo z zrcaljenjem eksponentne funkcije preko premice .
Primer 5.17: Graf funkcije ( , )
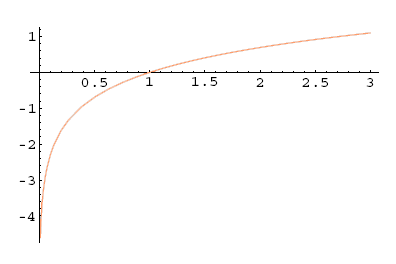
Slika 5.23:
***
5.3 Limita in zveznost
5.3.1 Limita
Definicija 5.18: Naj bo funkcija definirana v vsaki točki okolice to čke , razen morda v sami točki . število imenujemo limita funkcije v točki , če za vsak obstaja tako število , da je , če za vsak velja . To zapišemo
Zapisano drugače:
***
Primer 5.19:
1. Naj bo dana funkcija s predpisom . Potem je
.
2. Naj bo dana funkcija s predpisom . Potem je
***
Limita z leve in z desne
Definicija 5.20: Naj bo funkcija definirana na intervalu . število je limita z desne (desna limita) funkcije v točki , če za vsak obstaja tako število , da za vsak velja . To zapišemo:
***
Definicija 5.21: Naj bo funkcija definirana na intervalu . število je limita z leve (leva limita) funkcije v točki , če za vsak obstaja tako število , da za vsak velja . To zapišemo:
Funkcija ima v točki limito natanko tedaj, ko ima v točki limito z leve in z desne in sta ti dve limiti enaki.
***
Primer 5.22
Naj bo
Potem je
Ker leva in desna limita nista enaki, sledi, da funkcija v točki nima limite (slika 5.24).
Slika 5.24: Funkcija
***
Primer 5.23: Naj bo .
Iz grafa funkcije opazimo, da je
Iz tega sledi
in zato
Ker desna in leva limita nista enaki, funkcija nima limite v točki .
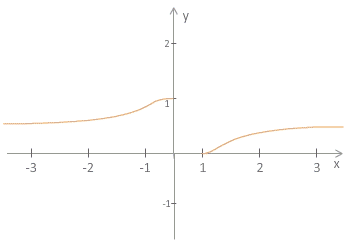
Slika 5.25:
***
Definicija 5.24: Naj bo definirana na intervalu . Funkcija ima limito , ko gre proti neskončno, če za vsak obstaja tak , da je izpolnjen za vsak . Torej
***
Definicija 5.25: Naj bo definirana na intervalu . Funkcija ima limito , ko gre proti negativni neskončnosti, če za vsak obstaja tak , da je izpolnjen za vsak . Torej
***
Izrek 5.26: Naj bo in naj bo . Potem velja:
(i) |
(ii) |
(iii) , če je . |
Zapišimo nekaj pomembnejših limit:
1. |
2. |
3. |
4. |
5. |
6. |
7. |
***
Primer 5.27:
1. Izračunajmo
2. Izračunajmo
***
5.3.2 Zveznost
Definicija 5.28: Naj bo funkcija definirana na okolici točke . Pravimo, da je zvezna v točki , če za vsak obstaja tako število , da je če je .
Krajši zapis:
je zvezna v .
V definiciji zveznosti funkcije v točki se skrivajo tri zahteve:
1. obstajati mora limita , |
2. funkcija mora biti definirana v točki , |
3. . |
***
Definicija 5.29: Funkcija je zvezna, če je zvezna v vsaki točki domene .
Če ni zvezna v , potem velja ena izmed možnosti:
1. v nima limite, |
2. v ima limito, vendar ni enaka . |
***
Izrek 5.30: Če sta funkciji in zvezni v točki , potem so zvezne tudi funkcije , , , , .
***
Primer 5.31:
Naj bo
Potem je
in .
Iz tega sledi, da funkcija ni zvezna v točki (slika 5.26).
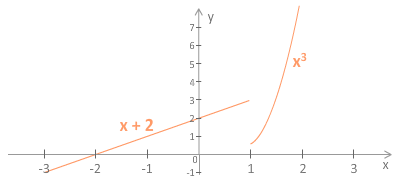
Slika 5.26: Funkcija
***
Zveznost z leve in z desne
Definicija 5.32: Funkcija , definirana na intervalu , je zvezna z desne v točki , če je njena vrednost enaka limiti z desne. Torej .
***
Definicija 5.33: Funkcija , definirana na intervalu , je zvezna z leve v točki , če je njena vrednost enaka limiti z leve. Torej .
Funkcija je zvezna v točki natanko tedaj, ko je v tej točki zvezna z leve in z desne.
***
Zveznost na intervalu
Definicija 5.34: Funkcija je zvezna na intervalu , če je: zvezna v vsaki točki in je zvezna z desne v točki ter je zvezna z leve v točki . Zapisano drugače:
Oznaka: zvezne funkcije na zaprtem intervalu
***
Izrek 5.35: Naj bo in naj bo . Potem obstaja tak , da je .
***
Definicija 5.36: Funkcija je na intervalu navzgor omejena, če obstaja tak , da je
Funkcija je navzdol omejena, če obstaja tak , da je
Pravimo, da je zgornja meja, pa spodnja meja funkcije na intervalu .
Funkcija je na intervalu omejena, če je navzgor in navzdol omejena.
***
Definicija 5.37: Najmanjša zgornja meja funkcije je natančna zgornja meja oziroma
Največja spodnja meja funkcije je natančna spodnja meja oziroma
Opomba:
***
Izrek 5.38: Vsaka zvezna funkcija je omejena.
***
Definicija 5.39: Naj bo . če je natančna zgornja meja funkcije tudi funkcijska vrednost, potem je maksimum funkcije na :
če je natančna spodnja meja funkcije tudi funkcijska vrednost, potem je minimum funkcije na :
***
Primer 5.40:
1. Naj bo , . Potem je
2. Naj bo , . Potem je
Očitno in ne obstajata.
3. Naj bo , . Potem je
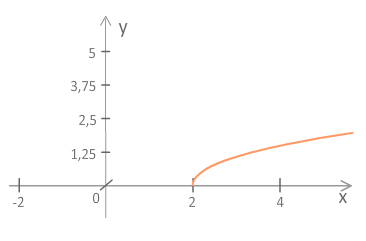
Slika 5.27:
***
Izrek 5.41: Zvezna funkcija doseže na intervalu minimum in maksimum.
***
Izrek 5.42: Zvezna funkcija zavzame vse vrednosti med minimumom in maksimumom.
***
5.4 Vprašanja
• Kdaj je funkcija soda? Podajte primer.
• Kdaj je funkcija liha? Podajte primer.
• Kdaj je funkcija naraščajoča?
• Kdaj je funkcija padajoča?
• Podajte primer monotone funkcije.
• Naj bo , , . Kaj so ničle polinoma ? Glede na diskriminanto zapišite vse možne primere.
• Opišite: trigonometrijske funkcije, ciklometrične funkcije, eksponentnme funkcije in logaritemske funkcije?
• Narišite grafe: trigonometrijskih funkcij, eksponentnih funkcij in logaritemskih funkcij.
• Naj bo funkcija definirana v okolici točke . Kdaj ima funkcija limito v točki ?
• Kdaj ima funkcija limito z leve v točki ?
• Kdaj ima funkcija limito z desne v točki ?
• Kdaj je funkcija zvezna v točki ?
• Kdaj je funkcija omejena? Podajte primer omejene funkcije?